Persamaan Logarima

Pengertian Persamaan Logaritma

Persamaan logaritma adalah persamaan yang memuat bentuk logaritma dengan basis atau numerus, atau keduanya memuat variabel. Jadi maksudnya, ada dua bentuk logaritma (di ruas kiri dan kanan) dimana basis atau numerus atau keduanya memuat variabel, kemudian kedua ruas ini dihubungan dengan tanda sama dengan. Nilai x yang memenuhi persamaan ini disebut dengan penyelesaian dari persamaan tersebut.

Sebelumnya, masih inget kan sama bentuk umum logaritma yang ini:

alog x = n

a = basis atau bilangan pokok, dengan syarat a > 0 dan a≠1
x = numerus, dengan syarat x > 0

n = nilai logaritma 

Bentuk-Bentuk Persamaan Logaritma

Nggak jauh beda dari materi eksponen, persamaan logaritma juga punya beberapa bentuk yang bikin kamu lebih gampang untuk mengidentifikasi nilai peubahnya. Nah, ini dia bentuk-bentuk persamaan logaritma:

Bentuk Umum Persamaan Logaritma

Secara umum, bentuk umum persamaan logaritma dibagi menjadi lima. Perbedaan ketiga persamaan terletak pada bentuk basis dan numerusnya. Adapun bentuk umum persamaan logaritma adalah sebagai berikut.

Bentuk Umum ^alog f(x) = ^alog g(x)

Bentuk umum pertama berlaku untuk dua persamaan yang memiliki basis yang sama, namun fungsi numerusnya berbeda. Bentuk umum yang dimaksud adalah sebagai berikut.

Dengan :

a = basis (bilangan pokok); dan

f(x) dan g(x) = numerus dalam bentuk fungsi.

Adapun contoh bentuk umum ^alog f(x) = ^alog g(x) adalah ²log(2x + 1) = ²log(x² – 1).

Agar suatu persamaan logaritma bisa terdefinisi, nilai numerus harus lebih besar dari nol. Artinya, solusi persamaan harus mengacu pada syarat tersebut.

Bentuk Umum ^alog f(x) = ^alogk

Bentuk umum kedua berlaku untuk dua logaritma dengan basis yang sama, di mana salah satu numerusnya berupa fungsi dan numerus yang lain berupa konstanta. Bentuk umum yang dimaksud adalah sebagai berikut.

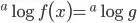
Dengan :

a = basis (bilangan pokok);

f(x)= numerus dalam bentuk fungsi; dan

k = numerus dalam bentuk konstanta.

Contoh penerapan bentuk umum ^alogf(x) = ^alogk adalah ³log(2x + 1) = ²log4.

Dari persamaan tersebut, numerus di ruas kiri berupa fungsi (2x + 1), sementara numerus di ruas kanan berupa konstanta, yaitu 4.

Bentuk Umum ^alog f(x) = ^blog f(x)

Bentuk umum ketiga berlaku untuk persamaan yang memiliki basis berbeda, namun numerus nya sama. Bentuk umum yang dimaksud adalah sebagai berikut.

Bentuk ini terpenuhi jika a ≠ b. Contoh bentuk ^alogf(x) = ^blogf(x) adalah sebagai berikut.

⁴log(2x + 1) = ⁵log(2x + 1)

Jika kamu menjumpai persamaan seperti di atas, bagaimana cara menentukan nilai x nya? Untuk tahu itu, simak sifat-sifat logaritma di sesi setelahnya , ya.

Bentuk Umum ^f(x)log g(x) = ^f(x)log h(x)

Bentuk umum keempat ini berlaku untuk persamaan logaritma dengan basis dan numerus berupa fungsi, di mana fungsi basisnya sama. Adapun bentuk yang dimaksud adalah sebagai berikut.

^f(x)log g(x) = ^f(x)log h(x)

Dengan :

f(x)= basis berupa fungsi; dan

g(x) dan h(x) = numerus dalam bentuk fungsi.

Yuk, perhatikan contoh bentuk umum ^f(x)log g(x) = ^f(x)log h(x) berikut ini.

^x+1log(3x – 4) = ^x+1log(5x)

Jika kamu menjumpai persamaan seperti di atas, lihat kembali sifat-sifat log beserta syaratnya, ya.

Bentuk Umum ^f(x)log h(x) = ^g(x)log h(x)

Bentuk umum kelima ini berlaku untuk persamaan yang kedua basisnya berupa fungsi berbeda, namun numerusnya sama. Adapun bentuk yang dimaksud adalah sebagai berikut.

^f(x)log h(x) = ^g(x)log h(x)

Contoh persamaan yang termasuk dalam bentuk umum kelima ini adalah sebagai berikut.

^x+1log(3x – 4) = ^x+2log(3x – 4)