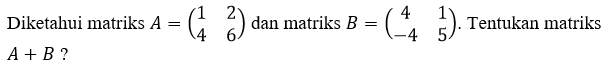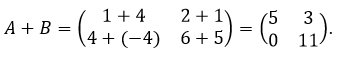Pengertian Operasi Matriks
Apa itu operasi matriks? Operasi matriks adalah operasi terhadap dua atau lebih matriks. Operasi matriks juga dikenal sebagai operasi aljabar matriks. Pada dasarnya, operasi matriks itu meliputi penjumlahan, pengurangan, dan perkalian matriks.
Operasi Penjumlahan Matriks
Contoh:
Hasil dari A + B dapat diperoleh dengan menjumlahkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.
Tentukan hasil penjumlahan pada matriks X dan Y!
Operasi Pengurangan Matriks
Pada dasarnya, pengurangan sama halnya dengan penjumlahan terhadap lawan bilangan penambah, sehingga pengurangan matriks A dengan matriks B dapat diartikan sebagai penjumlahan matriks A dengan lawan matriks B.
A – B = A + (-B)
Sama halnya dengan syarat penjumlahan matriks, dua atau lebih matriks hanya dapat dikurangkan apabila memiliki ordo yang sama, teman-teman. Nah, supaya kamu nggak bingung, kita coba kerjakan contoh soal di bawah ini, yuk. Gaasss~
Contoh:
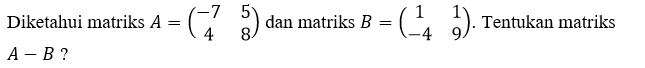
Hasil dari A – B dapat diperoleh dengan mengurangkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.
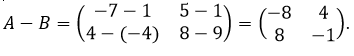
Jika matriks X - Y = Z, maka tentukanlah matriks Z!
Operasi Perkalian Matriks
Perkalian suatu matriks dengan skalar dapat dilakukan tanpa syarat tertentu. Artinya, semua matriks dengan ordo sembarang dapat dikalikan dengan bilangan real (skalar).
1. Operasi Perkalian Matriks dengan Bilangan Real (Skalar)
Perkalian matriks dengan bilangan real (skalar) tidak memiliki persyaratan. Jadi, semua matriks dengan ordo apapun bisa dikalikan dengan bilangan real (skalar).
bilangan d x Matriks C =
Secara garis besar, jika kamu ingin mengalikan matriks dengan bilangan real (skalar), maka berlaku sifat perkalian seperti:
1. Sifat distributif
C1 = Skalar ke 1, C2 = Skalar ke 2, X = Matriks ke 1, Y = Matriks ke 2
Berikut contoh soal perkalian matriks:
Contoh Soal:
Tentukan hasil dari a) 4A - 2B, jika matriks A dan B adalah:
Maka
2. Operasi Perkalian Dua Matriks
Pada pembahasan sebelumnya, kita sudah mengetahui bagaimana cara mengalikan matriks dengan bilangan real (skalar). Sekarang, kita akan membahas operasi perkalian dua matriks. Berikut rumus menghitung operasi perkalian dua matriks.
Operasi perkalian dua matriks memiliki beberapa sifat, yaitu:
A. Tidak Komutatif
Operasi perkalian dua matriks bersifat tidak komutatif. Artinya, berbeda dengan perkalian pada umumnya.
Contoh Soal:
Tentukan nilai AB dan BA, jika matrik A dan B adalah:
Jawab:
Sedangkan, matriks BA hasilnya sebagai berikut:
Jawab:
Bisa dilihat hasil keduanya berbeda, kan? Oleh karena itu, ini membuktikan bahwa sifat tidak komutatif pada perkalian matriks adalah benar.
B. Sifat Distributif
Pada sifat distributif ini berkaitan dengan operasi penjumlahan matriks. Berikut contohnya:
X (Y + Z) = XY + XZ
(Y + Z) X = YX + ZX
Contoh soal operasi perkalian matriks dengan sifat distributif:
Contoh Soal:
Tentukanlah hasil X (Y+Z) jika matriks X, Y, dan Z adalah sebagai berikut:
Jawab:
Rumus Sifat Matriks = X (Y + Z) = XY + XZ
